Mathematical Physics

Friday January 22 (S8)

11:00-11:30
Heinz Siedentop (Ludwig-Maximilians-Universität München)
Density-Matrix Functionals: Asymptotic Behavior of the Energy

We will show that a class of density matrix functionals introduced by Müller and others which describe correlated systems yield atomic energies which differ only by o(Z^5/3), Z the atomic number, from the infimum of the spectrum of the corresponding Schrödinger operator.

11:30-12:00
Egorova Iryna (B. Verkin Institute for Low Temperature Physics, Kharkiv)
The Cauchy problem for the KdV equation with steplike finite-gap initial data

Let $p_\pm(x,t)$ be two arbitrary finite-gap solutions of the the Korteweg-de Vries equation q_t = -q_xxx + 6 q q_x.

By means of the inverse scattering transform we solve the initial value problem for the KdV equation with smooth initial data q(x,0), which are asymptotically close to $p_\pm(x,0)$ in the following sense:

$$(q^{(s)}(x,0) - p_\pm^{(s)}(x,0))\vert x\vert^{m}\in L^1(\mathbb{R}_\pm)\quad \mbox{as} \quad\leq 0\leq s\leq n.$$

If the perturbation is sufficiently smooth ($n\geq 13$) and has a sufficient number of moments finite, $8\leq m\leq n -5$, then the classical solution q(x,t) of the KdV equation exists, is unique, and belongs to the class

$$(q^{(s)}(x,t) - p_\pm^{(s)}(x,t))\vert x\vert^{\lfloor\frac{m... ...L^1(\mathbb{R}_\pm)\quad \mbox{ with} \quad 0\leq s\leq n-m-2.$$

In particular, this implies that the solution remains in the Schwartz class of perturbations provided the initial condition is in this class.

Joint work with Katrin Grunert and Gerald Teschl.

12:00-12:30
Katrin Grunert (University of Vienna)
Long-time asymptotics for the Korteweg-de Vries equation

One of the most famous examples of completely integrable wave equations is the Korteweg-de Vries equation, q_t(x,t)=6q(x,t)q_x(x,t)-q_xxx(x,t), which can be solved via the inverse scattering method. We will consider decaying initial data and show how the inverse scattering problem can be reformulated as a Riemann-Hilbert problem. Based on this we will present how to extract long-time asymptotics by using the nonlinear steepest descent method.

14:00-14:30
David Krejčiřík ( Academy of Sciences, Prague )
The Hardy inequality and the asymptotic behaviour of the heat equation in twisted domains

In this talk we revise a recently established Hardy inequality in twisted tubes on the background of transience of the Brownian motion. We begin by recalling the classical Hardy inequality and its relation to geometric, spectral, stochastic and other properties of the underlying Euclidean space. After discussing the complexity of the problem when reformulated for quasi-cylindrical subdomains, we focus on the prominent class of tubes. As the main result, we show that the geometric deformation of twisting yields an improved decay rate for solutions of the heat equation in three-dimensional tubes of uniform cross-section. This is a joint work with Enrique Zuazua.

14:30-15:00
Takuya Mine ( Kyoto Institute of Technology )
Spectrum of the Aharonov-Bohm Hamiltonian with constant magnetic fields in the hyperbolic plane

We consider the Schrödinger operator H in the hyperbolic plane with the magnetic field given by the sum of a constant times the surface form and a finite number of the Dirac $\delta$ measures. Since the corresponding classical system contains both bounded orbits and unbounded ones, the spectrum of H contains both the continuous spectrum and infinitely degenerated eigenvalues (Landau levels). In the presence of the $\delta$ magnetic fields, there also exist a finite number of eigenvalues of finite multiplicity. We give an upper bound for the number of eigenvalues (counting multiplicity) between two successive Landau levels.

15:00-15:30
Oleksiy Kostenko ( Dublin Institute of Technology )
1-D Schrödinger operators with local point interactions

Spectral properties of 1-D Schrödinger operators

$$\mathrm{H}_{X,\alpha}:=-\frac{\mathrm{d}^2}{\mathrm{d} x^2} + \sum_{x_{n}\in X}\alpha_n\delta(x-x_n)$$

with local point interactions on a discrete set $X=\{x_n\}_{n=1}^\infty$ are well studied when $d_*:=\inf_{n,k\in\mathbb{N}}\vert x_n-x_k\vert>0$ (numerous results as well as a comprehensive list of references may be found in the monograph of Albeverio, Gesztesy, Hoegh-Krohn, Holden, Solvable Models in Quantum Mechanics, AMS Chelsea Publ., 2005; see also a survey of recent result given by Exner in Appendix K).

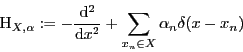
In the case d_*=0, it is only known that the operator $\mathrm{H}_{X,\alpha}$ may be symmetric with nontrivial deficiency indices (the example of Shubin Christ and Stolz, J. Math. Anal. Appl. 184 (1994)).

The main aim of our talk is the spectral analysis of the operators $\mathrm{H}_{X,\alpha}$ in the case d_*=0. We show that spectral properties of the operators $\mathrm{H}_{X,\alpha}$ correlate with the corresponding spectral properties of certain classes of unbounded Jacobi matrices. We exploit this connection to investigate self-adjointness, lower semiboundedness, and discreteness of the operators with local point interactions.

The talk is based on the joint work with Mark Malamud.

The work is supported by IRCSET Post-Doctoral Fellowship Program.