Zeta functions and enumerative problems over finite fields

Tibor Beke

Hungarian Academy of Sciences, Budapest

Suppose one has an enumerative combinatorial problem that can be evaluated over the finite fields with $q$, $q^2$, $q^3$, ... $q^k$ elements, giving rise to the sequence of counts $N_1$, $N_2$, $N_3$, ... $N_k$. When is the associated generating function

$$g(t) = \sum_{k=1}^\infty N_k t^k$$

a rational function?

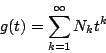
Part of the Weil conjectures (ie the theorem of Grothendieck-Deligne) is that if one counts the number of common zeroes of a set of polynomials over bigger and bigger finite fields, then the associated generating function is rational. We review the cohomological proof and subsequent extensions: to counting problems that involve first-order quantifiers (due to Kiefe, Macintyre and others) and field extensions (due to Wan). I continue with my own work, and mention some open problems.