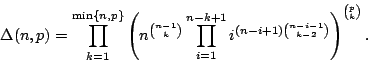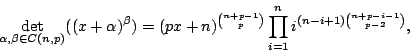A polynomial power-compositions determinant
Departament de Matemàtica Aplicada II
Universitat Politècnica de Catalunya
C. Pau Gargallo, 5. E-08028 Barcelona, Catalonia, Spain
Josep.M.Brunat@upc.edu
Let 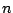 and
and 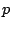 be positive integers. A
be positive integers. A
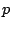 -composition of
-composition of 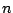 is a
is a 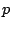 -tuple of non-negative integers
-tuple of non-negative integers
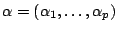 such that
such that
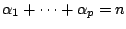 .
Denote by
.
Denote by 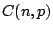 the set of
the set of 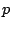 -compositions of
-compositions of 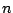 . If
. If
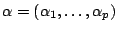 and
and
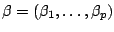 are
are 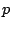 -compositions of
-compositions of
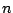 , we denote
, we denote
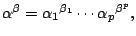 where to be consistent, it is assumed that
where to be consistent, it is assumed that 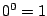 . The power-compositions
determinant is the determinant
. The power-compositions
determinant is the determinant
The value of 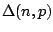 is given in [1]:
is given in [1]:
Recently, C. Krattenthaler in the complement [3] to
its impressive Advanced Determinant Calculus[2],
has given an equivalent formula
for 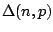 and has stated the following conjecture supported by computer experiments:
and has stated the following conjecture supported by computer experiments:
where 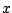 is a variable and
is a variable and 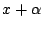 is short
for
is short
for
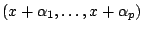 . In this talk we prove this conjecture
using a method that can be useful for other combinatorial determinants.
. In this talk we prove this conjecture
using a method that can be useful for other combinatorial determinants.
Footnotes
- ... Brunat1
- joint work with Antonio Montes
2005-05-23
![]() and
and ![]() be positive integers. A
be positive integers. A
![]() -composition of
-composition of ![]() is a
is a ![]() -tuple of non-negative integers
-tuple of non-negative integers
![]() such that
such that
![]() .
Denote by
.
Denote by ![]() the set of
the set of ![]() -compositions of
-compositions of ![]() . If
. If
![]() and
and
![]() are
are ![]() -compositions of
-compositions of
![]() , we denote
, we denote
![]() where to be consistent, it is assumed that
where to be consistent, it is assumed that ![]() . The power-compositions
determinant is the determinant
. The power-compositions
determinant is the determinant