Pro snažší hledání prací podle autora, názvu nebo sekce použijte seznam prací.
V případě špatné čitelnosti rovnic v abstraktu na webu, prosím použijte následující dokument ve formátu pdf - svocabst.pdf.
Dynamical systems generated by Darboux Baire-1 functions
Michaela Čiklová
MÚ Slezská Univerzita Opava
Ročník: 4.
Vedoucí práce: Prof. RNDr. Jaroslav Smítal, DrSc.
Abstrakt:
In 2001, Csörnyei, O'Neil and Preiss proved that the
composition of any two Darboux Baire-1 functions  possesses a fixed point, solving a long-standing open
problem. As a consequence, in 2003 Szuca proved that for such
functions the Sharkovsky theorem is satisfied. In this paper we
define topological entropy for Darboux Baire-1 functions using the
Bowen's approach, and show that this entropy has most of the usual
properties. In particular, the variational principle is true, and
consequently, topological entropy is supported by the set of
recurrent points. As the main result we prove that, similarly as
for the continuous maps of the interval, a Darboux Baire-1
function has positive topological entropy if and only if it has a
cycle of period different from possesses a fixed point, solving a long-standing open
problem. As a consequence, in 2003 Szuca proved that for such
functions the Sharkovsky theorem is satisfied. In this paper we
define topological entropy for Darboux Baire-1 functions using the
Bowen's approach, and show that this entropy has most of the usual
properties. In particular, the variational principle is true, and
consequently, topological entropy is supported by the set of
recurrent points. As the main result we prove that, similarly as
for the continuous maps of the interval, a Darboux Baire-1
function has positive topological entropy if and only if it has a
cycle of period different from  . To do this
we develop theory of recurrent, . To do this
we develop theory of recurrent, 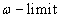 , and nonwandering
points of such functions since, in general, the standard results
from the topological dynamics, are not true: For example, there is
a Darboux Baire-1 function f such that neither the set of
recurrent points nor the set of , and nonwandering
points of such functions since, in general, the standard results
from the topological dynamics, are not true: For example, there is
a Darboux Baire-1 function f such that neither the set of
recurrent points nor the set of 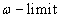 points of f are
invariant. points of f are
invariant.
Bifurkácie kodimenzie 1 pre kvadratické a kubické autonómne systémy diferenciálnych rovníc
Hriňák Martin
Fakulta matematiky, fyziky a informatiky Univerzity Komenského v Bratislave
Ročník: 5.
Vedoucí práce: Prof.RNDr. Milan Medveď, DrSc.
Abstrakt:
V tejto práci sú študované niektoré dvojrozmerné a trojrozmerné autonómne
systémy obyčajných diferenciálnych rovníc. Kvadratický systém je analyzovaný
podrobnejšie, analyzuje sa počet singulárnych bodov tohto systému, ich typ,
bifurkácie kodimenzie 1 a hľadajú sa limitné cykly tohto systému. Analýza kubického
systému je obmedzená na zisťovanie existecie periodických trajektórií. Aplikácia dosiahnutých
výsledkov je možná v uvedenom neokeynesovskom IS-LM modeli. Anylýza periodických
trajektórií trojrozmerného autonómneho systému sa robí pomocou redukcie na centrálnu varietu.
Obmedzuje sa však len na popísanie postupu, keďže získané vzťahy medzi jednotlivými
parametrami sú značne rozsiahle. Zároveň sa pri jednotlivých systémoch ukazuje, že
Poincerého-Andronovova veta sa práve pri systémoch tohto typu nedá aplikovať.
Quasilinear hyperbolic equation with hysteresis operator
Petra Kordulová
MÚ Slezská Univerzita Opava
Ročník: 5.
Vedoucí práce: RNDr. Jana Kopfová, Ph.D.
Abstrakt:
We consider quasilinear hyperbolic equations
with a hysteresis operator. Firstly, the hysteresis
operator is a simple play with given boundary condition.
Later the same hysteresis model is considered but
the boundary condition is changed. Some special examples
of the generalized play operators are mentioned.
An explicit solution for an elementary example is given.
This paper is based on the example which is solved in [7].
But here more complicated boundary condition is taken,
the solution is computed in detail and some special
examples of the play operators are given.
Jemné vlastnosti sobolevovských funkcí
Pavel Podbrdský
MFF UK Praha
Ročník: 6.
Vedoucí práce: Prof. RNDr. Jan Malý, DrSc.
Abstrakt:
Věta o záměně proměnných v Lebesgueově integrálu je jedním ze základních
nástrojů matematické analýzy. Její různá zobecnění patří mezi velmi studované
oblasti matematiky. Jednou ze zajímavých otázek je najít co nejobecnější třídu
přechodových zobrazení u, pro které věty daného typu platí. Je-li
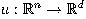 sobolevovská funkce (tj. existují-li všechny slabé parciální
derivace funkce u, které jsou navíc reprezentovatelné lokálně
integrovatelnými funkcemi), daná problematika vede na zkoumání chování funkce
u na množinách nulové míry a na tzv. m-coarea vlastnost.
sobolevovská funkce (tj. existují-li všechny slabé parciální
derivace funkce u, které jsou navíc reprezentovatelné lokálně
integrovatelnými funkcemi), daná problematika vede na zkoumání chování funkce
u na množinách nulové míry a na tzv. m-coarea vlastnost.
V naší práci se danou problematikou zabýváme v obecnosti zobrazení
 ,
kde X a Y jsou metrické prostory; prostor X je navíc vybaven doubling
mírou m. V této obecnosti je potřeba najít náhradu za pojem gradientu v
eukleidovských prostorech. Jednou z možností je pojem (slabého) horního
gradientu.
,
kde X a Y jsou metrické prostory; prostor X je navíc vybaven doubling
mírou m. V této obecnosti je potřeba najít náhradu za pojem gradientu v
eukleidovských prostorech. Jednou z možností je pojem (slabého) horního
gradientu.
V první kapitole seznamujeme čtenáře s úvodem do dané problematiky, nastiňujeme
motivace jednotlivých problémů, směry zkoumání a uvádíme některé články, které
se danou problematikou zabývají.
Ve druhé kapitole uvádíme základní definice, značení a základní tvrzení, které
budeme používat. Dále definujeme Lorentzovy prostoru
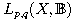 funkcí s
hodnotami v reálném Banachově prostoru
funkcí s
hodnotami v reálném Banachově prostoru
 a uvádíme základní tvrzení pro
práci s nimi.
a uvádíme základní tvrzení pro
práci s nimi.
Ve třetí kapitole zavádíme a zkoumáme vlastnosti newtonovských prostorů
 funkcí
funkcí
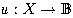 které mají horní gradient v
Lorentzově prostoru
které mají horní gradient v
Lorentzově prostoru
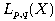 Newtonovské prostory tvoří jeden z možných přístupů
k definici sobolevovských prostorů v této obecnosti.
Newtonovské prostory tvoří jeden z možných přístupů
k definici sobolevovských prostorů v této obecnosti.
Ukazujeme, že tyto
newtonovské prostory jsou Banachovy a za jistých předpokladů ukazujeme, že
množina lipschitzovských funkcí je v nich hustá. To nám dává možnost dokázat
odhad pro kapacitu množiny nelebesgueovských bodů funkcí z těchto prostorů.
Výsledky o newtonovských prostorech jsou nové pro
 Ve čtvrté kapitole ukazujeme, že za předpokladu platnosti (1,p)-Poincarého
nerovnosti pro některé p<m (resp. pro p=m za dodatečných předpokladů na
kvalitu prostoru X) precizně reprezentované funkce
Ve čtvrté kapitole ukazujeme, že za předpokladu platnosti (1,p)-Poincarého
nerovnosti pro některé p<m (resp. pro p=m za dodatečných předpokladů na
kvalitu prostoru X) precizně reprezentované funkce
 které mají
horní gradient v prostoru
které mají
horní gradient v prostoru
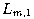 splňují m-coarea vlastnost. To zlepšuje
výsledek z článku [M1], kde je zmíněné tvrzení dokázáno za silnějšího
předpokladu (1,1)-Poincarého nerovnosti. Navíc ukazujeme, že funkce z
prostoru
splňují m-coarea vlastnost. To zlepšuje
výsledek z článku [M1], kde je zmíněné tvrzení dokázáno za silnějšího
předpokladu (1,1)-Poincarého nerovnosti. Navíc ukazujeme, že funkce z
prostoru
 lze precizně reprezentovat a tedy tyto funkce mají "dobré"
reprezentanty, které m-coarea vlastnost splňují.
lze precizně reprezentovat a tedy tyto funkce mají "dobré"
reprezentanty, které m-coarea vlastnost splňují.
Tato práce je mírně upravenou verzí diplomové práce autora. Nemá žádou
souvislost s pracemi spolupodanými autorem do dřívějších ročníků soutěže SVOČ.
Asymptotické chování řešení parciálních diferenciálních rovnic na neomezených prostorových intervalech
Lukáš Poul
MFF UK Praha
Ročník: 5.
Vedoucí práce: RNDr. Eduard Feireisl, DrSc.
Abstrakt:
V práci studujeme asymptotické chování řešení kvazilineární evoluční rovnice
 se zadanou nezápornou počáteční podmínkou a homogenní Dirichletovou okrajovou
podmínkou. Hlavním výsledkem je důkaz existence řešení, které provelké časy konverguje k prostorově lokalizované vlně stacionárního řešení cestující
do nekonečna.
se zadanou nezápornou počáteční podmínkou a homogenní Dirichletovou okrajovou
podmínkou. Hlavním výsledkem je důkaz existence řešení, které provelké časy konverguje k prostorově lokalizované vlně stacionárního řešení cestující
do nekonečna.
Podokázání dobré určenosti problému, tj. existence, jednoznačnosti řešení, se
v práci věnujeme analýze existence a jednoznačnosti netriviálního
integrovatelného řešení příslušného stacionárního problému na  ,
tzv. ground state solution. Dále zobecníme některé výsledky teorie
koncentrované kompaktnosti na případ kvazilineárních rovnic.
Hlavní výsledek je poté dokázán s přispěním teorie tzv. nulových bodů. ,
tzv. ground state solution. Dále zobecníme některé výsledky teorie
koncentrované kompaktnosti na případ kvazilineárních rovnic.
Hlavní výsledek je poté dokázán s přispěním teorie tzv. nulových bodů.
Hlavní výsledek je netriviálním zobecněním tvrzení známého pro semilineární
rovnice. Při jeho důkazu byla zobecněna tvrzení známá pro případ semilineárních
rovnic.
Práce je mírnou modifikací autorovy diplomové práce.
Související odkazy:
|
