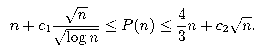|
S3 - Matematické struktury |
|---|---|
SVOČ 2004SoutěžOrganizaceInformace
|
Pro snažší hledání prací podle autora, názvu nebo sekce použijte seznam prací. V případě špatné čitelnosti rovnic v abstraktu na webu, prosím použijte následující dokument ve formátu pdf - svocabst.pdf. Algebraické a predalgebraické zvazy
In this work we deal with algebraic and pre-algebraic lattices that are denoted
as (Q) and (K). We show the relation between the classes (Q) and (K). We also study
some operators on these classes, for example direct product and dual lattice. We prove,
e.g. that classes (Q) and (K) are closed under operator of the direct product. On the other
hand, we show that these classes are not closed under the operator of the dual lattice.
Moduly konečně projektivní dimenze
Tato práce se zabývá moduly konečně projektivní a injektivní dimenze.
Uvádíme některá základní fakta o těchto modulech a vyvíjíme nástroje pro práci s nimi.
Pro
On the longest alternating path connecting points on a circle
Let n be a positive integer and let n red and n blue points lie on a circle
at the vertices of a convex 2n-gon. For
On list chromatic number of cartesian product of two graphs
Given a list L(v) of colours for each vertex v of graph G, we say that a
vertex colouring is acceptable if every vertex is coloured with a colour on its list and no
two adjacent vertices are assigned the same colour. The list chromatic number of a graph
G, denoted
Choosability of graphs with infinite sets of forbidden differences
We study the notion of the list-T-coloring which is a common generalization
of the T-coloring and the list-coloring. Given a graph G, a set of non-negative integers T
and a list-assignment L for each vertex of G, the graph G is said to be T-colorable from
the list-assignment L if there exists a coloring c such that the color c(v) of each vertex
v is contained in its list L(v) and
Využitie Gröbnerových báz na dôkazy viet elementárnej geometrie Touto prácou predstavujeme teóriu Gröbnerových báz v okruhoch polynómov viacerých premenných. Popisujeme základné vlastnosti redukcie a usporiadania termov, dôvod existencie a algoritmus na nájdenie bázy. Poukazujeme na jednoznačnost' redukovanej Gröbnerovej bázy. Ukazujeme využitie Gröbnerových báz pri dokazovaní viet elementárnej geometrie pomocou výpočtovej techniky. Využívame pritom postup navrhnutý Kapurom. Základom je preformulovanie geometrického problému pomocou analytickej geometrie do polynomického tvaru a následné určenie doplňujúcich podmienok. Účinnost' tejto metódy prezentujeme na riešení geometrických dôkazových úloh posledných dvadsiatich ročníkov Medzinárodnej matematickej olympiády. The simplest subspace of generators of the 2x2-matrix algebra M2(C) and of the 3x3-matrix algebra M3(C) The simplest subspaces of generators of the complex 2×2 and 3×3 - matrix algebras are found. Simplicity is measured by the number of parameters in the free resolution of the algebra. The result for 2×2 - matrices was presented at the competition SVOČ in Banská Bystrica last year and provided Clifford generators (Pauli matrices) as a solution. The problem of the 3×3-matrix algebra M3(C) is not a straightforward extension of the case M2(C), as there are no Clifford generators. It is shown here that another well-known subspace of generators, the Lie algebra su(2) provides the solution. This work will be submitted as the author’s diploma thesis. Steinerovské farbenie kubických grafov
Farbenie kubického grafu pomocou steinerovského systému trojíc je farbenie jeho hrán tak, aby farby každej trojice hrán majúcej spoločný vrchol tvorili trojicu steinerovského systému. Hlavným výsledkom mojej práce je, že kubické grafy bez sériovoparalelného konca (t.j. všetky steinerovsky zafarbitel'né grafy vöbec) sú zafarbitel'né steinerovským systémom AG(1,3)×PG(2,2) rádu 21. Ďalej sa podarilo úplne charakterizovat' triedu kubických grafov zafarbitel'ných afínnymi steinerovskými systémami AG(n, 3) pre
Charakterizácia triedy minimálnych 4-geodeticky súvislých grafov Graf G nazývame k-geodeticky súvislý (k-GC), k > 0, ak je súvislý a je potrebné odstránit' aspoň k vrcholov na to, aby sa zvätšila vzdialenost' medzi nejakými dvoma vrcholmi, alebo sa G zredukoval na jediný vrchol, alebo sa G stal nesúvislým. Minimálny k-GC graf má najmenší počet hrán spomedzi všetkých k-GC grafov s rovnakým počtom vrcholov. V tejto práci definujeme triedu tzv. k-ticových grafov, ktorá je základom pre triedy minimálnych k-GC grafov a charakterizujeme triedu minimálnych 4-GC grafov. Tilting modules over artin algebras An existence of tilting modules is in many cases ensured by well-known theoretical results. But their inner structure is often still under investigation. In this work we give an explicit description of the structure of a family of 1-tilting modules over a finite dimensional algebra by Igusa, Smalo and Todorov, where the presently known results could not be applied. Also, we describe the lattice of all tilting classes of a finite type over this algebra; and we give examples of modules from a tilting class, which are not reachable from finitely generated modules of the same tilting class by direct limits. As a means for achieving these results, we show a general version of the Auslander-Reiten formula. Finally, we outline a possible approach for investigating the conjecture that every 1-tilting class is of a finite type for a large family of rings. In particular, we show that a finite type of a given 1-tilting class cannot be determined by looking only at its pureinjective modules. This work uses main results of my diploma work. Komplexita a balance nekonečného slova odpovídajícího kvadratickým Pisotovým číslům
Při daném
Související odkazy:
|
-noetherovské okruhy dokážeme, že každý modul projektivní dimenze nejvýše n má
a jak N' tak M/N' mají injektivní dimenzi nejvýše n (
, a sequence
of
segments is called an alternating path of length k, if
are pairwise different
vertices of the 2n-gon, every segment
connects points of different
colors and no two segments
,
intersect at inner point.
Let P(n) be the maximum number such that for every configuration of n red and n blue
points there exists an alternating path of length at least P(n). We show that there exist
positive constants n0, c1, c2 such that for every n > n0 
, is a minimum r, which satisfies: if every list has at least r members
then there is an acceptable colouring. Let colouring number of graph G, denoted col(G),
be
. We deal with a problem formulated by M. Borowiecki and
S. Jendrol’:
denote list chromatic number of G and let
be the Cartesian
product of graphs G and H. Does there exist an absolute constant c such that
. If answer is YES, how big is c? Does
c = 1 ?
. For arbitrary graphs G and H we prove a weaker upper bound
. In the second part we bound list
chromatic number of
for arbitrary graph G asymptotically as follows:
for
for any two adjacent vertices u and
v. The T-choice number of a graph G number is the minimum integer k such that G is
T-colorable for any list-assignment L which assigns each vertex of G a list of at least k
colors.
lze každé nezáporné číslo reprezentovat tzv.
-rozvojem,
který představuje zobecnění běžného vyjádření čísel v desítkové soustavě. Jsou-li v tomto
rozvoji všechny koeficienty u záporných mocnin
nulové, hovoříme o
, pak příslušné slovo je balancované a rovněž byl stanoven vztah pro komplexitu. V případě jiných kvadratických Pisotových čísel byl podán důkaz, že balanční funkce (viz dále) je omezená, nicméně její horní mez (tedy ani optimální horní mez) nebyla známa; komplexita nebyla prozkoumána vůbec.
, které
je kořenem polynomu
. Provedeme úvahy nad strukturou jemu příslušejícího
nekonečného slova, za pomocí kterých nalezneme explicitní tvar funkce vyjadřující komplexitu.
Dále stanovíme optimální horní mez balanční funkce; konkrétně ukážeme, že se
jedná o 2-balancované slovo.
není Pisotovým číslem; je známo, že potom není balanční
funkce příslušného nekonečného slova omezená. Bude podán vlastní důkaz neomezenosti.