Pro snažší hledání prací podle autora, názvu nebo sekce použijte seznam prací. V případě špatné čitelnosti rovnic v abstraktu na webu, prosím použijte následující dokument ve formátu pdf - svocabst.pdf.

Minimaxové kritérium ve finančním rozhodování
Jana Čerbáková
MFF UK Praha
Ročník: 5.
Vedoucí práce: Prof. RNDr. Jitka Dupačová, DrSc.

Abstrakt:

Tato práce je věnovaná minimaxovému kritériu a vybraným aplikacím při řešení úloh stochastického programování s finanční tématikou. Vychází ze stejnojmenné diplomové práce. Minimaxové kritérium je úspěšné zejména v situacích s neúplnou znalostí pravděpodobnostních rozdělení náhodných proměnných.

V první části je představena minimaxová úloha stochastického programování a je vyslovena zobecněná minimaxová věta. Detailnější pohled je věnován momentovému problému a jeho zobecněné variantě pro diskretní případ, který nebyl v práci Shapiro, Ahmed (2003), z níž bylo čerpáno, uveden.

V druhé kapitole je definován pojem kvalitativní informace jakožto znalosti o uspo-řádání velikostí pravděpodobností rúzných variant budoucího vývoje náhodných paramentrů. Vlastním přínosem je důkaz poslední věty této kapitoly, v níž jsou formulovány vlastnosti krajních bodů množin pravděpodobnostních rozdělení konzistentních s nějakou kvalitativní informací.

Závěrečná kapitola se soustřeďuje na řešení úloh s kvalitativní informací o diskrétním pravděpodobnostním rozdělení. Výsledkem je algoritmus založený na postupech zpětné rekurze. Který byl opraven oproti Bühlerova postupu (1973). Uveden je také konkrétní výpočet pro zadanou modelovou situaci a další možné zobecnění, v němž se použijí výsledky zobecněného momentového problému pro danou třídu úloh s kvalitativní informací.

Toeplitzovy matice a plurální čísla ve statistické analýze časových řad
Karel Hron
PF Univerzity Palackého Olomouc
Ročník: 4.
Vedoucí práce: prof. RNDr. Ing. Lubomír Kubáček, DrSc. Dr.h.c.

Abstrakt:

Cílem práce je zpracování kompletního postupu při odhadech chování periodických dat se šumem, jež je stacionárním procesem. Pro zpřesnění délek period, určených z periodogramu, a neznámých parametrů lineárního modelu je navíc oproti standardnímu postupu využito též dvou iteračních procesů. V jednom z nich s vypočtenou Toeplitzovou varianční maticí je při vyčíslení její inverse využito aritmetiky prvku lokálního okruhu plurální algebry pro zefektivnení výpočtu při použití nejobecnějšího vzorce. Plurální čísla dosud nebyla mimo oblast geometrické algebry aplikována. Získané postupy jsou posléze úspešně aplikovány při řešení reálného příkladu z oblasti maloobchodních řetězců, kde byly tyto metody zpracování dat pro problémy s velkým zašumením souboru použity, pokud je autorovi známo, vůbec poprvé.

Předkládaná práce byla oceněna 1. místem ve fakultním kole SVOČ 2004. Ve své diplomové práci se autor v současné době zabývá vlastnostmi řešení soustav lineárních rovnic nad plurálními čísly.

Některé aspekty regulace pojistných rizik
Petr Jedlička
MFF UK Praha
Ročník: 5.
Vedoucí práce: Prof. RNDr. Tomáš Cipra, DrSc.

Abstrakt:

V této práci popíšeme regulaci pojistných rizik prostřednictvím kapitálových požadavků. Ta je prováděna za účelem ochrany zájmů klientů před případnou nesolventností pojišťovny. Pojistná rizika nabývají totiž v současném světě stále vyššího objemu, a proto splnění adekvátně formulovaných kapitálových opatření pojistného dozoru může výrazně přispět (vedle např. transferu pojistných rizik na finanční trhy) k finanční stabilitě pojišťovny.

Práce prezentuje nejprve matematické a statistické principy odvození kapitálových požadavků ke splnění regulace s důrazem na podchycení principiálních rozdílů mezi evropským a americkým přístupem a se zřetelem na rozdíly vnímání rizika z pohledu dozorových orgánů (Risk Based Capital) a majitelů pojišťovny (Performance Based Capital). Užití odvozovaných principů a uváděných vztahů je ilustrováno na jednoduchých numerických příkladech. Pozornost je věnována i vztahům rizik v rámci finanční skupiny a s tím spojeným principům bankovních regulací podle Basilejské dohody.

V této oblasti se podařilo odvodit výsledky pro kapitálovou situaci holdingu a ty srovnat s odděleným monitorováním banky a pojišťovny. Ukázali jsme, za jakých situací je diverzifikace (holding má menší kapitálové požadavky než obě společnosti zvlášť) uskutečnitelná a matematicky jsme odvodili, jaký vliv na kapitálovou situaci mají jednotlivé účetní faktory. Získané výsledky jsme interpretovali v souladu s principy regulace.

Teoretická odvozování jsou na vhodných místech textu doplněna nejen ilustrativními příklady, ale i praktickými ukázkami, jak se solventnost opravdu s ohledem na doprovodnou legislativu skutečně vykazuje. Celá realizace je podrobněji popsána v mé diplomové práci. Tato práce je pouze její součástí.

Optimální přístup k segmentaci dat
Petr Novotný
MFF UK Praha
Ročník: 4.
Vedoucí práce: doc. Jaromír Antoch, CSc.

Abstrakt:

Úkolem je proložit vektor s mnoha pozorováními po částech spojitou regresní funkcí tak, aby regresní model v daném úseku spojitosti závisel pouze na datech v tomto úseku. Dále požadujme, aby počet bodů nespojitosti byl nejvýše K-1. Přitom chceme najít dělení, které minimalizuje zvolenou ztrátovou funkci, například residuální součet čtverců.

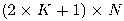Klasický algoritmus založený na~dynamickém programování má paměťovou náročnost , kde N je délka celého vektoru. V článku navržený algoritmus při zachování stejného počtu operací potřebuje pouze čísel vpaměti. Je-li regresní funkce po částech konstantní, lze snížit časovou složitost z na .

Tento článek se nijak nevztahuje k mé diplomové práci ani k jiným soutěžním pracem.

Minimální cesty semimartingalů
Libor Pospíšil
MFF UK Praha
Ročník: 5.
Vedoucí práce: prof. RNDr. Josef Štěpán, DrSc.

Abstrakt:

Soutěžní práce „Minimální cesty semimartingalů“ pojednává o úloze minimální cesty pro lokální martingaly a semimartingaly a o jejích aplikacích ve finanční matematice, přesněji v modelu trhu s cennými papíry.

Výchozím zdrojem pro tuto práci je část III publikace Dupačová J., Hurt J., Štěpán J. (2002): Stochastic Modeling in Economics and Finance (Kluwer Academic Publishers).

Vlastním přínosem práce je jednak přístup k problematice – nejprve je řešena samotná úloha minimální cesty pro lokální martingaly metodami stochastické analýzy (sekce 3.1). To umožňuje lépe vidět její podstatu a pokusit se o její zobecnění, což je druhý přínos práce – vyřešení úlohy za zeslabených předpokladů (sekce 3.2) oproti výše uvedené publikaci.

V dalších částech práce je popsán model pro spojitý trh s cennými papíry tak, aby v něm bylo možné úlohu minimální cesty s různými předpoklady interpretovat.

Tyto úlohy a modely jsou předstupněm k Black-Scholesově teorii oceňování opcí, která je dnes prakticky využívána ve finančních výpočtech.

Soutěžní práce je zkrácenou verzí mojí diplomové práce se stejným názvem „Minimální cesty semimartingalů“, v níž je navíc obsažena kapitola, která se týká Black-Scholesovy rovnice pro oceňování opcí.

Jak jsem se učil modelovat realitu
Luboš Prchal
MFF UK Praha
Ročník:
Vedoucí práce: doc. RNDr. Jaromír Antoch, CSc.

Abstrakt:

Předkládaná práce se zabývá statistickou analýzou závislosti intenzity radioaktivního záření na výšce nad zemským povrchem. V úvodní kapitole popisuje způsob měření a pohled meteorologů na analyzovaná data. Druhá kapitola je věnována hledání tvaru a parametrizace nelineárních regresních modelů vhodných k popisu vertikálních profilů radiace. Použití numerických metod pro odhad parametrů navrhovaných modelů a porovnání dostupného software se diskutuje v kapitole III. Výsledkům a srovnání odhadnutých modelů je pak věnována čtvrtá kapitola.

Tato práce ukazuje cestu, jak statistickými metodami modelovat a odhadnout fyzikálně zatím nepopsaný funkcionální vztah mezi radiací a nadmořskou výškou. Odhadnuté modely navíc můžeme chápat jako "vstupní" funkcionální data pro další statistické analýzy této problematiky; analýzy, které by měly odpovědět na aktuální meteorologické otázky, např. zda existuje sezónnost v chování radiokativity či jak identifikovat "odlehlá" pozorování.

Obsah předkládané analýzy se shoduje s kapitolou II diplomové práce Prchal L.: Neparametrické odhady pro analýzu funkcionálních dat. MFF UK, Praha, 2004.

Analýza dvojfaktorového modelu vývoja úrokovej miery so stochastickou volatilitou
Beata Stehlíková
Fakulta matematiky, fyziky a informatiky Univerzity Komenského v Bratislave
Ročník: 5.
Vedoucí práce: Doc.RNDr. Daniel Ševčovič, CSc.

Abstrakt:

V práci sa zaoberáme modelovaním vývoja okamžitej úrokovej miery a cenami dlhopisov, ktoré tento vývoj implikuje. Najskôr uvádzame jednofaktorový model. Kvôli väčším možnostiam pri zachytení možného priebehu výnosovej krivky sa do modelu pridáva druhá rovnica, ktorá predstavuje druhý zdroj náhodnosti. Dostávame sa tak k dvojfaktorovým modelom. V rámci nich sa zaoberáme modelom so stochastickou volatilitou. Druhým faktorom je tu proces riadiaci volatilitu. Oceˇnovanie dlhopisov vedie k parciálnej diferenciálnej rovnici, ktorú numericky riešime. Cena dlhopisu v tomto modeli závisí aj od hodnoty druhého faktora. Volatilita úrokovej miery však nie je pozorovatel’ná veličina, jej hodnoty sa teda nedajú priamo dosadzovat’ do riešenia. Preto navrhujeme postup na výpočet spriemernenia vzhl’adom na tento faktor. Odvodíme limitné rozdelenie skrytého procesu. Aproximujeme ho diskrétnym rozdelením nadobúdajúcim hodnoty, v ktorých máme numericky vypočítanú cenu dlhopisu. Použijeme ho na výpočet spriemernených cien dlhopisov a výnosových kriviek a ich intervalov spol’ahlivosti.

Srovnání metod klasifikace
Petr Vaněk
FSI VUT Brno
Ročník: 5.
Vedoucí práce: Doc. RNDr. Jaroslav Michálek, CSc.

Abstrakt:

V práci jsou porovnávány dvě metody klasifikace objektů. První je klasická metoda diskriminační analýzy, lineární i kvadratická. Druhá metoda je založena na využití zobecněného lineárního modelu a logistické regrese. Tyto dvě metody jsou porovnávány na simulovaných datech. Jako testovací data byly simulovány výběry z normálního rozdělení, dále kontaminované normální rozdělení a konečně speciální případy elipticko-vrstevnicového rozdělení. Metody jsou posuzovány podle četnosti chybně zařazených objektů. Práce je součástí diplomové práce.

Související odkazy:

• Práce v sekci S1 - Matematická analýza
• Práce v sekci S3 - Matematické struktury
• Práce v sekci S4 - Teoretická informatika
• Práce v sekci S5 - Aplikovaná matematika
• Seznam všech prací - podle sekcí